Understanding Data Structures and Algorithms - A Beginner's Guide

Have you ever wondered how computers organize information or solve complex problems quickly? The secret lies in two fundamental concepts in computer science: data structures and algorithms. In this guide, we’ll explore these topics in a way that’s easy to understand, even if you’re new to programming.

What Are Data Structures?

Imagine you’re organizing a big party. You need to keep track of your guests, the food you’ll serve, and the music playlist. How would you organize all this information? That’s where data structures come in!

Data structures are like special containers that help us store and organize data in our computer programs. They’re the digital equivalent of filing cabinets, bookshelves, or even that junk drawer in your kitchen (but much more organized, we promise!).

Why Do We Need Data Structures?

You might be wondering, “Can’t we just throw all our data into one big pile?” Well, we could, but that would be like trying to find a specific sock in a mountain of laundry. Data structures help us:

1. Keep our data tidy and easy to find
2. Work with our data more efficiently
3. Solve complex problems with less headache

Types of Data Structures

There are many types of data structures, each with its own superpowers. Let’s take a look at some of the most common ones and how they work for basic understanding:

1. Arrays
2. Linked Lists
3. Stacks
4. Queues
5. Trees
6. Graphs
7. Hash Tables

We’ll dive deeper into each of these as we go along.

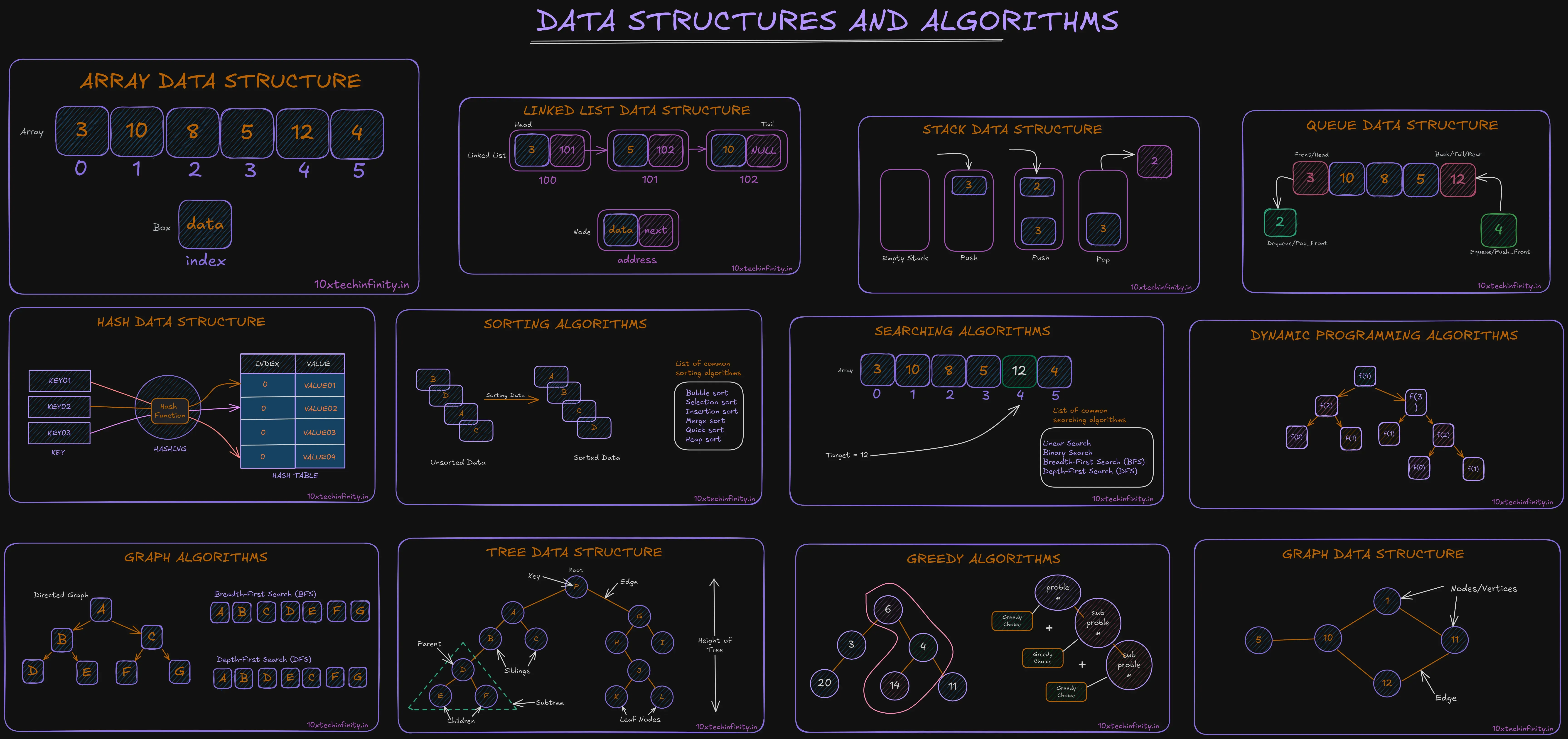
1. Arrays

An array is like a row of boxes, where each box can hold a piece of data. It’s simple and great for storing lists of items when you know how many items you’ll have.

How data is stored:

Data in arrays is stored in contiguous memory locations, which means all elements are placed next to each other in memory.

Why use arrays:

• Quick access to elements (if you know the position)
• Simple to use for small, fixed-size lists

Code example:

Array Sample Example

#include <iostream>
using namespace std;

int main() {
    // Declaring an array of integers with 5 elements
    int numbers[5];

    // Initializing array elements
    for(int i = 0; i < 5; i++) {
        numbers[i] = i * 10;
    }

    // Accessing and printing array elements
    for(int i = 0; i < 5; i++) {
        cout << "Element at index " << i << ": " << numbers[i] << endl;
    }

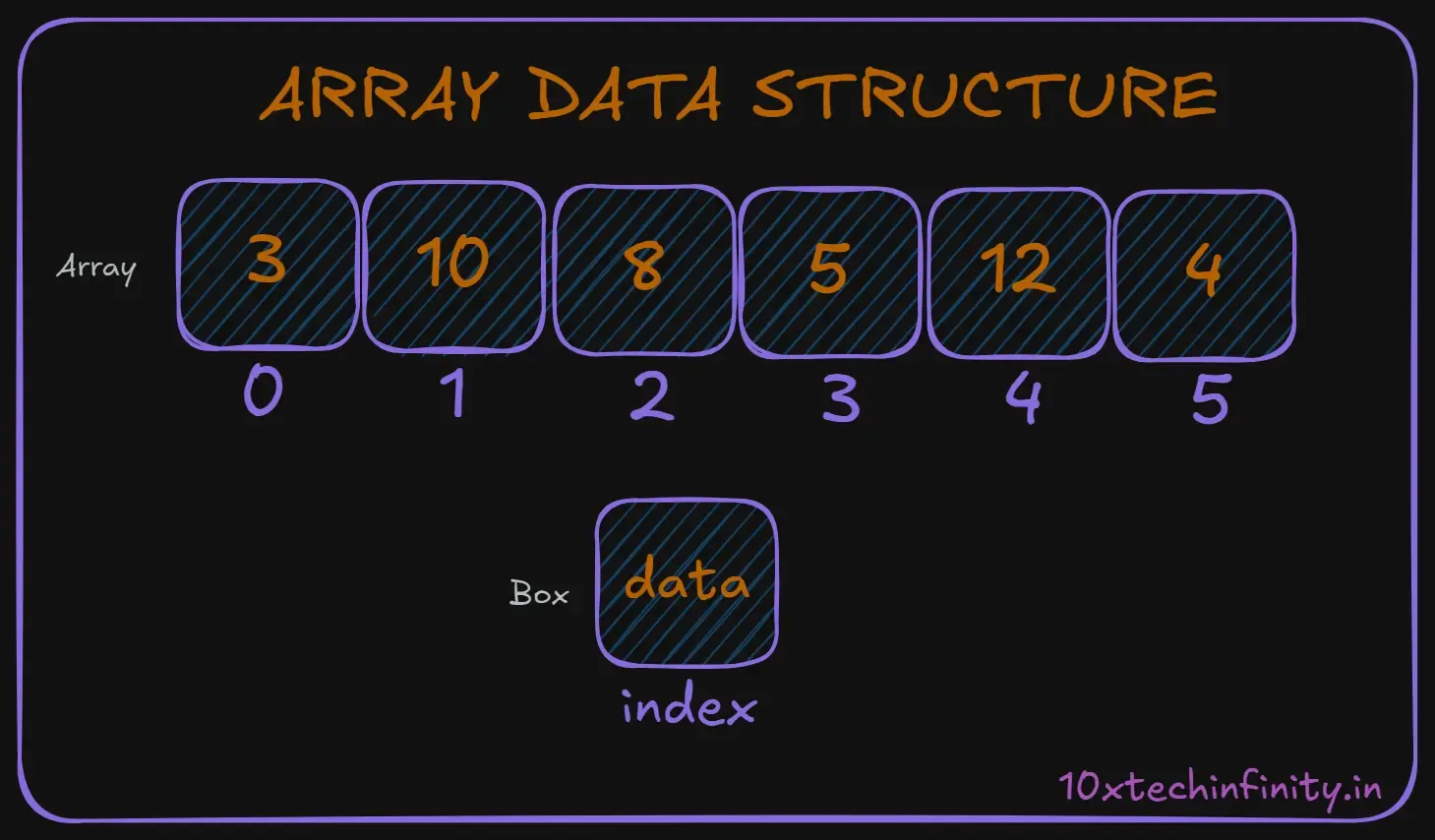
    return 0;
}

2. Linked Lists

A linked list is like a treasure hunt, where each item holds a clue to where the next item is. It’s great when you need to frequently add or remove items from the list.

How data is stored:

Each element (node) contains the data and a reference (or link) to the next element in the sequence.

Why use linked lists:

• Easy insertion and deletion of elements
• Dynamic size (can grow or shrink easily)

Code example:

Linked List Sample Example

#include <iostream>
using namespace std;

// Define the structure of a node
struct Node {
int data;
Node\* next;
};

int main() {
// Create the first node (head of the list)
Node\* head = new Node();
head->data = 1;
head->next = nullptr;

    // Add a second node
    Node* second = new Node();
    second->data = 2;
    second->next = nullptr;
    head->next = second;

    // Add a third node
    Node* third = new Node();
    third->data = 3;
    third->next = nullptr;
    second->next = third;

    // Traverse and print the linked list
    Node* current = head;
    while(current != nullptr) {
        cout << current->data << " -> ";
        current = current->next;
    }
    cout << "nullptr" << endl;

    return 0;

}

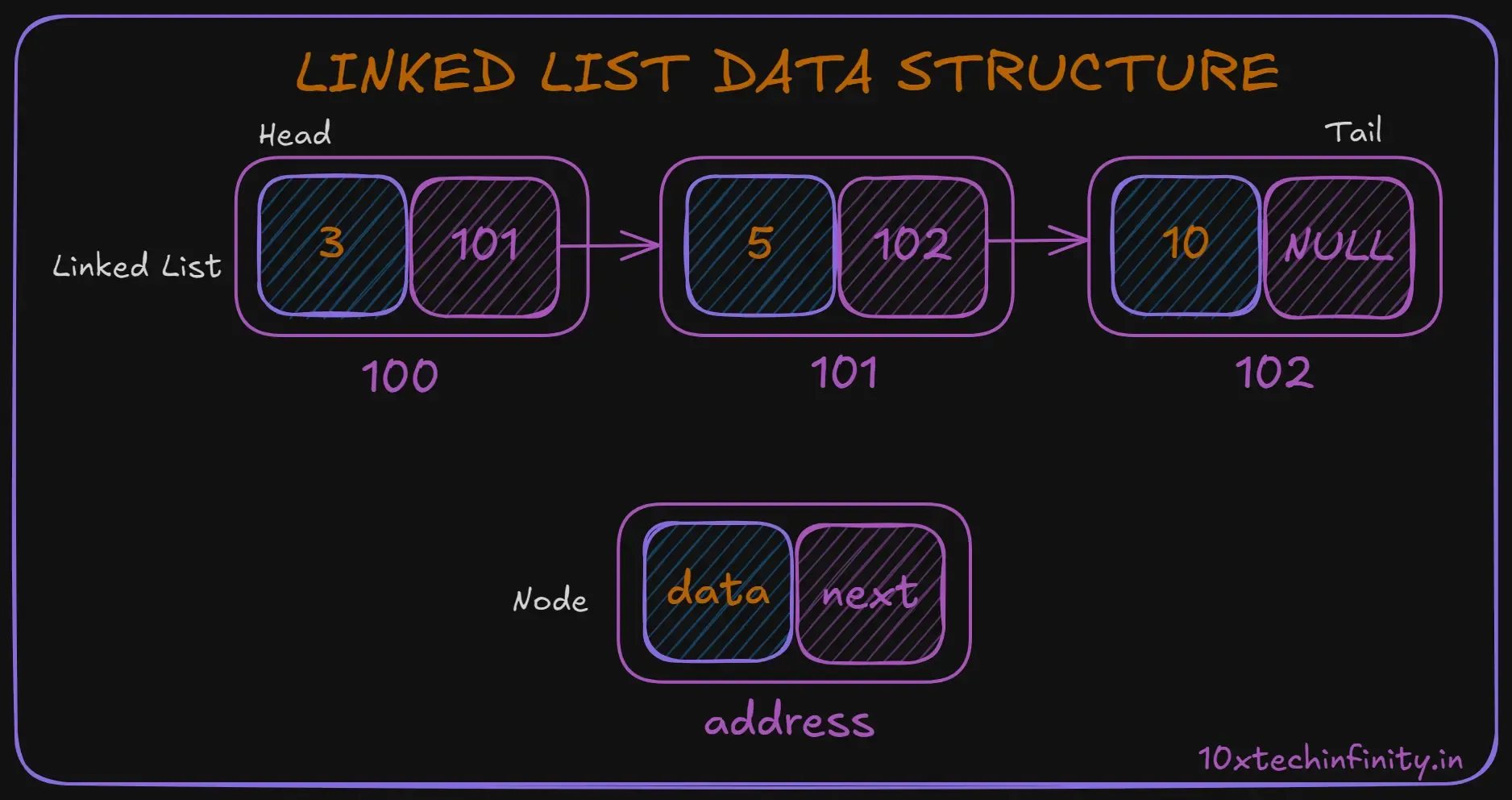
3. Stacks

A stack is like a pile of plates. You can only add or remove from the top. This “last in, first out” (LIFO) structure is useful for tracking things in reverse order.

How data is stored:

Elements are added and removed from the same end, called the “top” of the stack.

Why use stacks:

• Useful for reversing order of elements
• Helpful in function call management and expression evaluation

Code example:

Stack Sample Example

#include <iostream>
#include <stack>
using namespace std;

int main() {
    stack<int> myStack;

    // Pushing elements onto the stack
    myStack.push(10);
    myStack.push(20);
    myStack.push(30);

    // Accessing the top element
    cout << "Top element: " << myStack.top() << endl;

    // Popping elements from the stack
    while (!myStack.empty()) {
        cout << "Popped: " << myStack.top() << endl;
        myStack.pop();
    }

    return 0;
}

4. Queues

A queue is like a line at a movie theater. The first person to join the line is the first to enter the theater. This “first in, first out” (FIFO) structure is great for managing tasks in order.

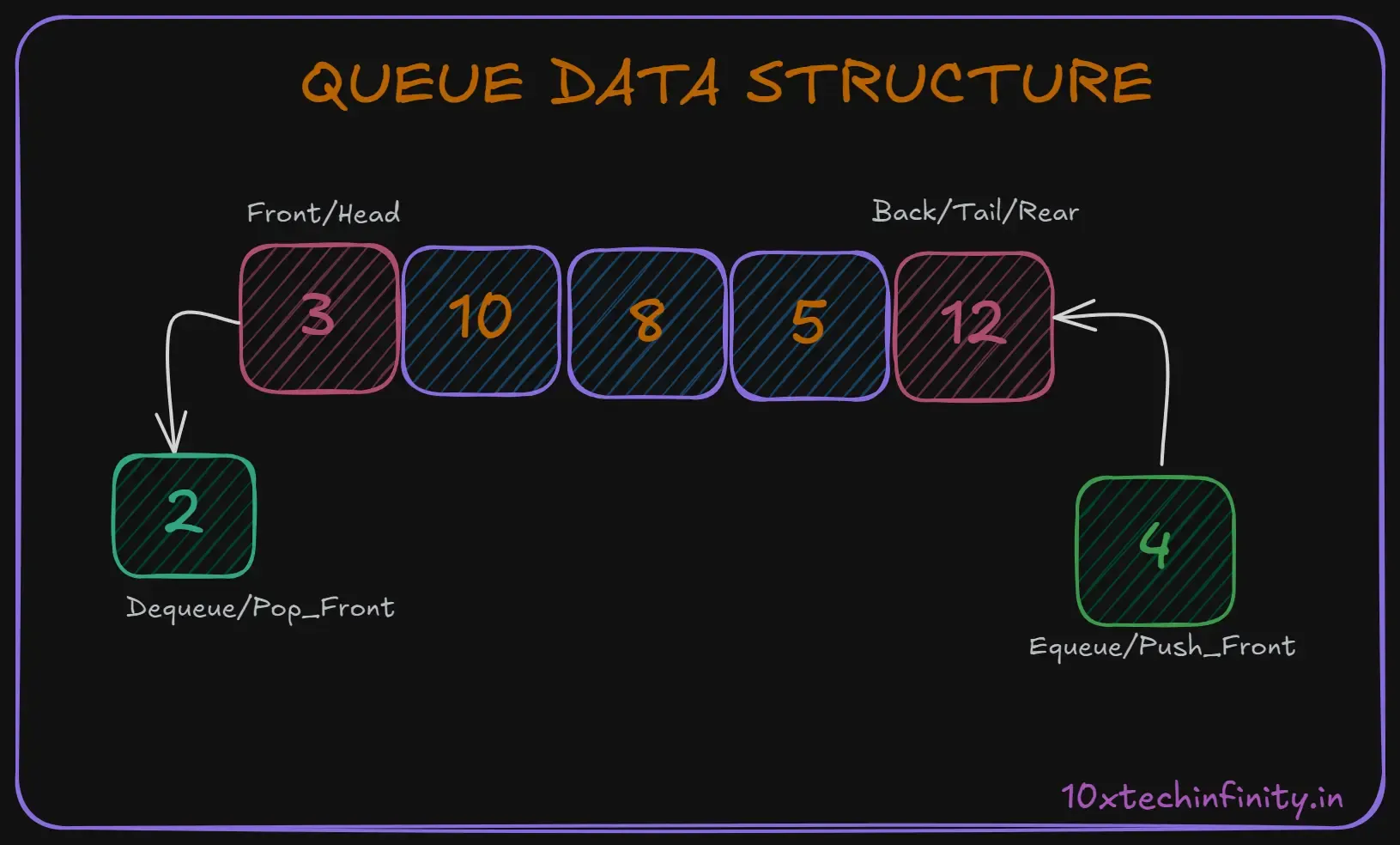
How data is stored:

Elements are added at one end (rear) and removed from the other end (front).

Why use queues:

• Useful for maintaining order of operations
• Helpful in scenarios like task scheduling or breadth-first search algorithms

Code example:

Queue Sample Example

#include <iostream>
#include <queue>
using namespace std;

int main() {
    queue<int> myQueue;

    // Enqueuing elements
    myQueue.push(10);
    myQueue.push(20);
    myQueue.push(30);

    // Accessing the front element
    cout << "Front element: " << myQueue.front() << endl;

    // Dequeuing elements
    while (!myQueue.empty()) {
        cout << "Dequeued: " << myQueue.front() << endl;
        myQueue.pop();
    }

    return 0;
}

5. Trees

A tree is like a family tree, with a root (the oldest ancestor) and branches (descendants). It’s great for representing hierarchical relationships.

How data is stored:

Each node in a tree can have child nodes, creating a hierarchical structure.

Why use trees:

• Efficient for searching and sorting
• Natural representation for hierarchical data

Code example (Binary Tree):

Binary Tree Sample Example

#include <iostream>
using namespace std;

struct Node {
    int data;
    Node* left;
    Node* right;
};

// Function to create a new node
Node* createNode(int data) {
    Node* newNode = new Node();
    newNode->data = data;
    newNode->left = newNode->right = nullptr;
    return newNode;
}

// Function to insert a node in the binary tree
Node* insertNode(Node* root, int data) {
    if (root == nullptr) {
        root = createNode(data);
        return root;
    }

    if (data < root->data) {
        root->left = insertNode(root->left, data);
    } else if (data > root->data) {
        root->right = insertNode(root->right, data);
    }

    return root;
}

// Function to perform inorder traversal
void inorderTraversal(Node* root) {
    if (root == nullptr) return;

    inorderTraversal(root->left);
    cout << root->data << " ";
    inorderTraversal(root->right);
}

int main() {
    Node* root = nullptr;

    // Inserting nodes
    root = insertNode(root, 50);
    insertNode(root, 30);
    insertNode(root, 20);
    insertNode(root, 40);
    insertNode(root, 70);
    insertNode(root, 60);
    insertNode(root, 80);

    // Performing inorder traversal
    cout << "Inorder traversal: ";
    inorderTraversal(root);
    cout << endl;

    return 0;
}

6. Graphs

A graph is like a map of cities and the roads connecting them. It’s perfect for representing complex relationships between items.

How data is stored:

Graphs consist of vertices (nodes) and edges (connections between nodes).

Why use graphs:

• Ideal for representing networks or relationships
• Useful in solving complex problems like shortest path algorithms

Code example (Adjacency List representation):

Graph Sample Example

#include <iostream>
#include <vector>
using namespace std;

class Graph {
private:
int V; // Number of vertices
vector<vector<int>> adj; // Adjacency list

public:
Graph(int v) : V(v), adj(v) {}

    // Function to add an edge to the graph
    void addEdge(int v, int w) {
        adj[v].push_back(w);
        adj[w].push_back(v); // For undirected graph
    }

    // Function to print the adjacency list
    void printGraph() {
        for (int v = 0; v < V; ++v) {
            cout << "Adjacency list of vertex " << v << ": ";
            for (auto x : adj[v]) {
                cout << x << " ";
            }
            cout << endl;
        }
    }

};

int main() {
Graph g(4);
g.addEdge(0, 1);
g.addEdge(0, 2);
g.addEdge(1, 2);
g.addEdge(2, 3);

    g.printGraph();

    return 0;

}

7. Hash Tables

A hash table is like a super-efficient filing system. It uses a special formula (hash function) to decide where to store each piece of data, making it very fast to find things later.

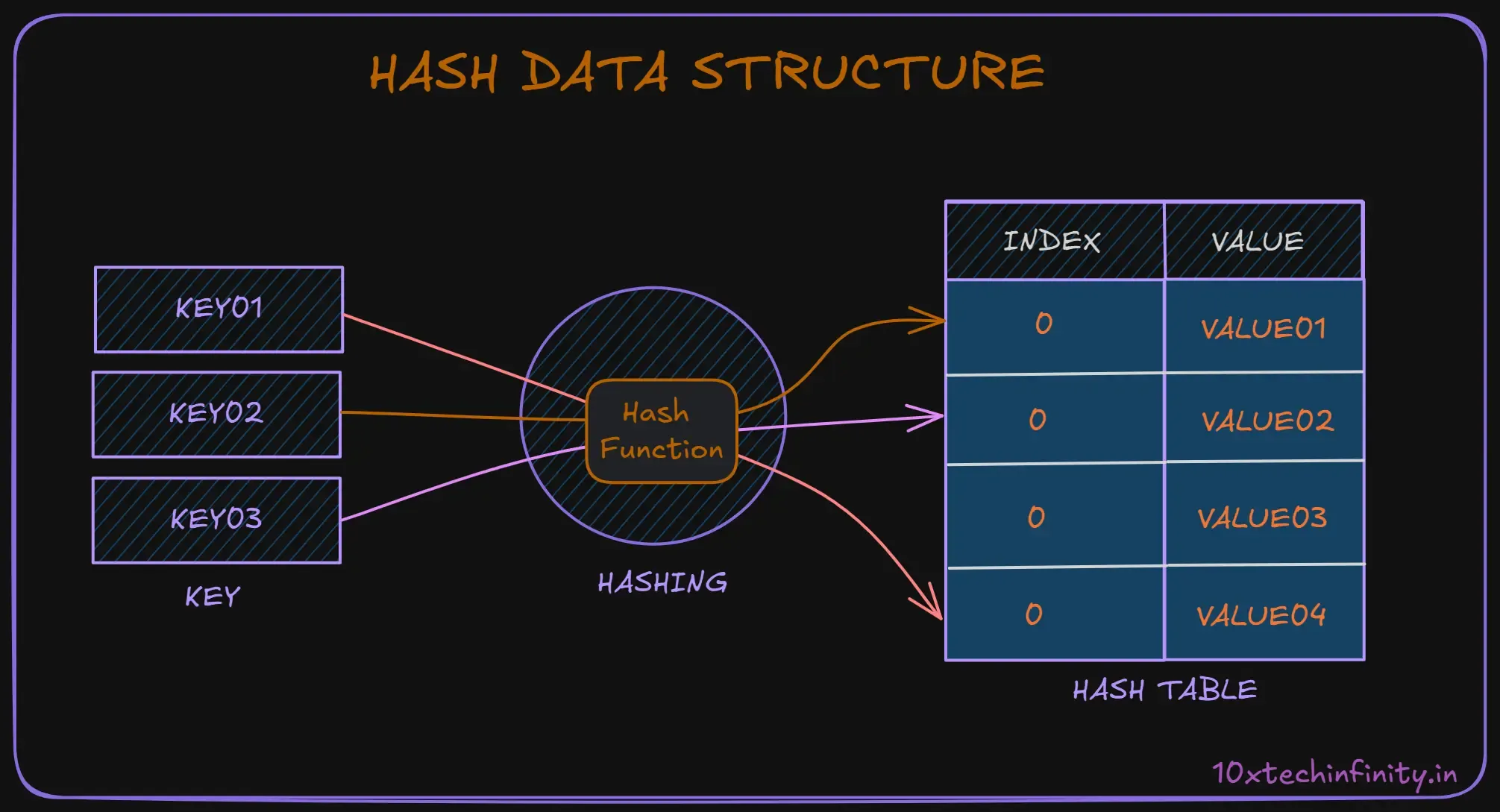
How data is stored:

Data is stored in an array, but the index is determined by a hash function applied to the key.

Why use hash tables:

• Very fast data retrieval
• Efficient for large datasets when the hash function is well-designed

Code example:

Hash Table Sample Example

#include <iostream>
#include <unordered_map>
#include <string>
using namespace std;

int main() {
    // Creating a hash table
    unordered_map<string, int> hashTable;

    // Inserting key-value pairs
    hashTable["apple"] = 5;
    hashTable["banana"] = 7;
    hashTable["orange"] = 3;

    // Accessing values
    cout << "Price of apple: $" << hashTable["apple"] << endl;

    // Checking if a key exists
    if (hashTable.find("grape") == hashTable.end()) {
        cout << "Grape not found in the hash table" << endl;
    }

    // Iterating through the hash table
    for (const auto& pair : hashTable) {
        cout << pair.first << ": $" << pair.second << endl;
    }

    return 0;
}

What Are Algorithms?

If data structures are like organizing systems, algorithms are like recipes. They’re step-by-step instructions for solving problems or performing tasks. Just as there are many ways to cook a meal, there are often multiple algorithms to solve a problem, each with its own advantages and trade-offs.

Example: Imagine you’re baking a cake. The recipe tells you what ingredients to use (that’s like the data structure) and how to mix and bake them (that’s the algorithm). Together, they help you create a delicious result!

Why Do We Need Algorithms?

Algorithms are crucial because they help us:

1. Solve problems efficiently
2. Save time and resources
3. Handle large amounts of data
4. Make our programs faster and smarter

Types of Algorithms

There are many types of algorithms, each designed to solve different kinds of problems. Some common types include:

1. Sorting algorithms
2. Searching algorithms
3. Graph algorithms
4. Dynamic programming algorithms
5. Greedy algorithms

We’ll explore these in more detail as we go through our learning journey. And Let’s explore some common types of algorithms:

1. Sorting Algorithms

Sorting algorithms arrange data in a specific order, like alphabetical or numerical. They’re crucial for organizing information efficiently.

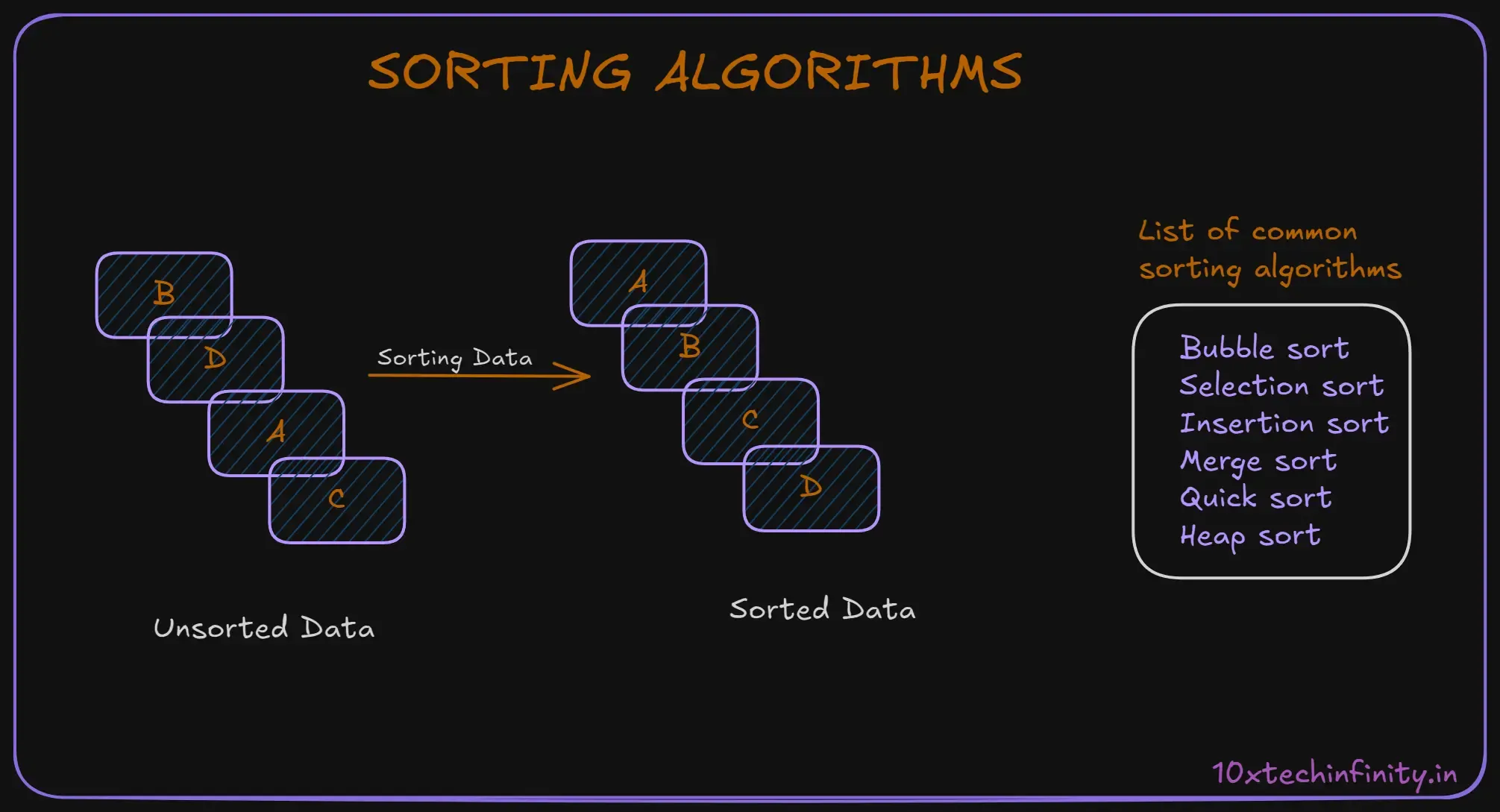
Example: Bubble Sort

Bubble Sort is a simple sorting algorithm that repeatedly steps through the list, compares adjacent elements and swaps them if they are in the wrong order.

Bubble Sort Example

#include <iostream>
using namespace std;

void bubbleSort(int arr[], int n) {
for (int i = 0; i < n-1; i++) {
for (int j = 0; j < n-i-1; j++) {
if (arr[j] > arr[j+1]) {
// Swap arr[j] and arr[j+1]
int temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
}
}
}
}

// Function to print an array
void printArray(int arr[], int size) {
for (int i = 0; i < size; i++)
cout << arr[i] << " ";
cout << endl;
}

int main() {
int arr[] = {64, 34, 25, 12, 22, 11, 90};
int n = sizeof(arr)/sizeof(arr[0]);

    cout << "Unsorted array: ";
    printArray(arr, n);

    bubbleSort(arr, n);

    cout << "Sorted array: ";
    printArray(arr, n);

    return 0;

}

2. Searching Algorithms

Searching algorithms help find specific items in a collection of data. They’re essential for quickly locating information.

Example: Binary Search

Binary Search is an efficient algorithm for searching a sorted array by repeatedly dividing the search interval in half.

Binary Search Example

#include <iostream>
using namespace std;

int binarySearch(int arr[], int l, int r, int x) {
    while (l <= r) {
        int m = l + (r - l) / 2;

        // Check if x is present at mid
        if (arr[m] == x)
            return m;

        // If x greater, ignore left half
        if (arr[m] < x)
            l = m + 1;

        // If x is smaller, ignore right half
        else
            r = m - 1;
    }

    // If we reach here, then element was not present
    return -1;
}

int main() {
    int arr[] = {2, 3, 4, 10, 40};
    int n = sizeof(arr) / sizeof(arr[0]);
    int x = 10;

    int result = binarySearch(arr, 0, n - 1, x);

    if (result == -1)
        cout << "Element is not present in array";
    else
        cout << "Element is present at index " << result;

    return 0;
}

3. Graph Algorithms

Graph algorithms solve problems related to graph structures, like finding the shortest path between two points or detecting cycles in a network.

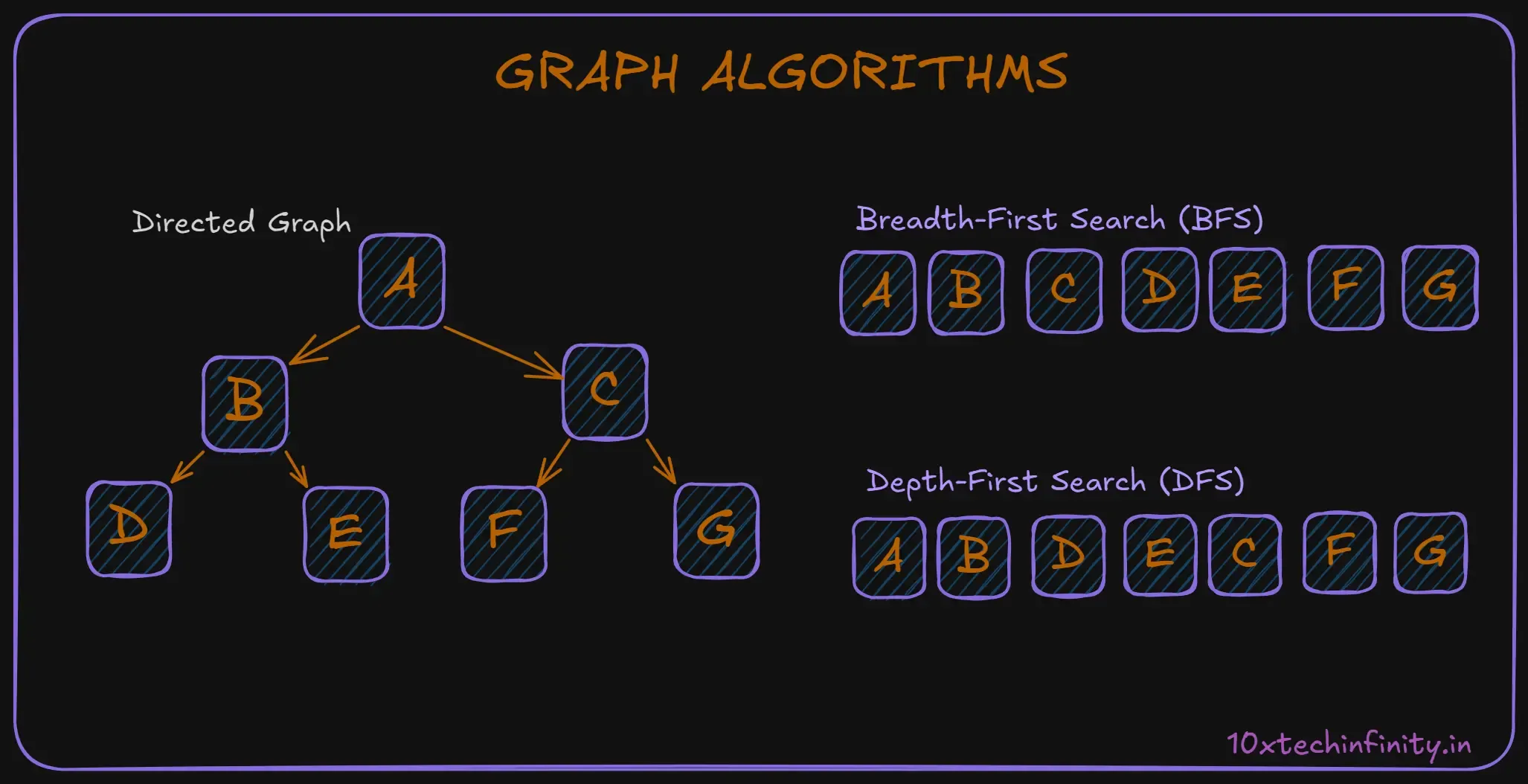
Example: Depth-First Search (DFS)

DFS is used to traverse or search tree or graph data structures. It starts at a root node and explores as far as possible along each branch before backtracking.

Depth-First Search Example

#include <iostream>
#include <vector>
using namespace std;

class Graph {
private:
int V; // Number of vertices
vector<vector<int>> adj; // Adjacency list

public:
Graph(int v) : V(v), adj(v) {}

    void addEdge(int v, int w) {
        adj[v].push_back(w);
    }

    void DFSUtil(int v, vector<bool>& visited) {
        // Mark the current node as visited and print it
        visited[v] = true;
        cout << v << " ";

        // Recur for all the vertices adjacent to this vertex
        for (int i : adj[v]) {
            if (!visited[i])
                DFSUtil(i, visited);
        }
    }

    void DFS(int v) {
        // Mark all the vertices as not visited
        vector<bool> visited(V, false);

        // Call the recursive helper function to print DFS traversal
        DFSUtil(v, visited);
    }

};

int main() {
Graph g(4);
g.addEdge(0, 1);
g.addEdge(0, 2);
g.addEdge(1, 2);
g.addEdge(2, 0);
g.addEdge(2, 3);
g.addEdge(3, 3);

    cout << "Depth First Traversal (starting from vertex 2): ";
    g.DFS(2);

    return 0;

}

4. Dynamic Programming Algorithms

Dynamic programming is a method for solving complex problems by breaking them down into simpler subproblems. It’s often used for optimization problems.

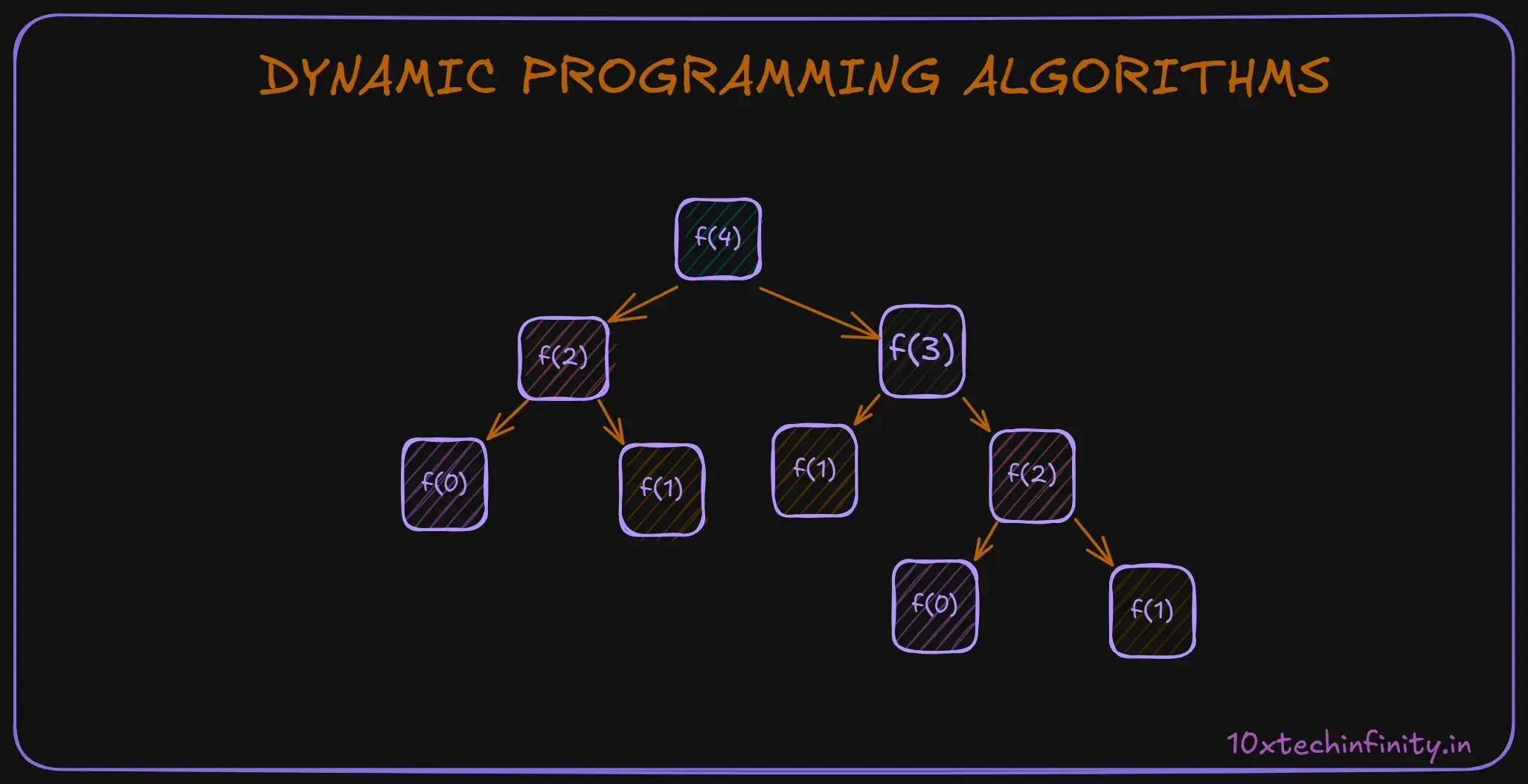
Example: Fibonacci Sequence

The Fibonacci sequence is a series of numbers where each number is the sum of the two preceding ones. Dynamic programming can efficiently calculate Fibonacci numbers.

Fibonacci Example

#include <iostream>
#include <vector>
using namespace std;

int fibonacci(int n) {
    // Base cases
    if (n <= 1)
        return n;

    // Create a vector to store Fibonacci numbers
    vector<int> fib(n + 1);
    fib[0] = 0;
    fib[1] = 1;

    // Calculate and store Fibonacci numbers
    for (int i = 2; i <= n; i++) {
        fib[i] = fib[i - 1] + fib[i - 2];
    }

    // Return the nth Fibonacci number
    return fib[n];
}

int main() {
    int n = 10;
    cout << "The " << n << "th Fibonacci number is: " << fibonacci(n) << endl;
    return 0;
}

5. Greedy Algorithms

Greedy algorithms make the locally optimal choice at each step, hoping to find a global optimum. They’re often used for optimization problems.

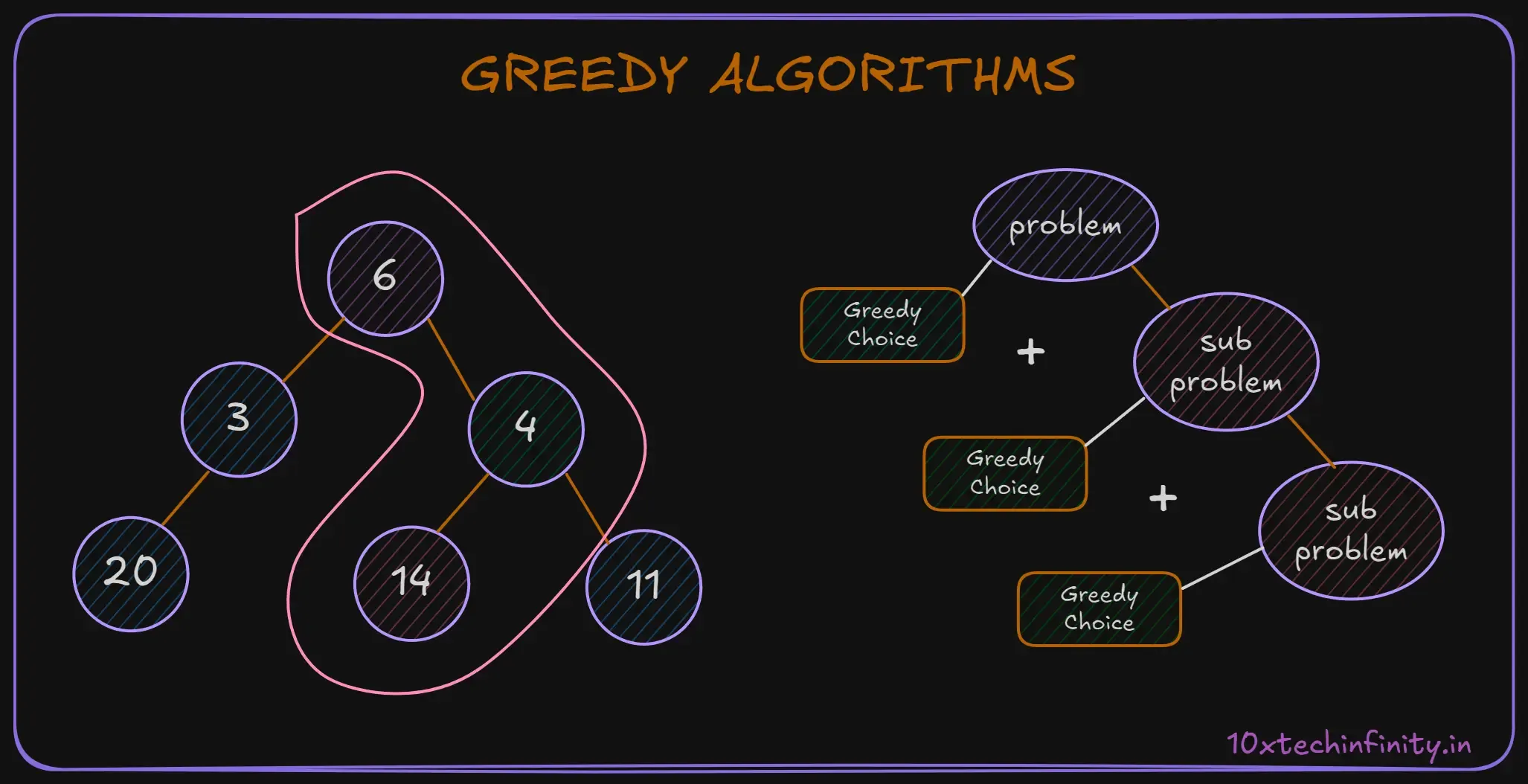
Example: Coin Change Problem

The coin change problem involves finding the minimum number of coins needed to make a certain amount of change.

Coin Change Example

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

int coinChange(vector<int>& coins, int amount) {
// Sort coins in descending order
sort(coins.rbegin(), coins.rend());

    int totalCoins = 0;

    for (int coin : coins) {
        // Use as many of the current coin as possible
        while (amount >= coin) {
            amount -= coin;
            totalCoins++;
        }

        // If we've made all the change, we're done
        if (amount == 0) {
            break;
        }
    }

    // If we couldn't make all the change, return -1
    return amount == 0 ? totalCoins : -1;

}

int main() {
vector<int> coins = {25, 10, 5, 1}; // Quarter, dime, nickel, penny
int amount = 67;

    int result = coinChange(coins, amount);

    if (result == -1) {
        cout << "It's not possible to make change for " << amount << " cents." << endl;
    } else {
        cout << "Minimum number of coins needed: " << result << endl;
    }

    return 0;

}

Why Are Data Structures and Algorithms Important?

1. Efficiency: Good data structures and algorithms can make your programs run faster and use less memory.
2. Problem-Solving: They provide proven solutions to common programming problems, saving you time and effort.
3. Scalability: As your programs handle more data, efficient data structures and algorithms become crucial for maintaining performance.
4. Interviews: Many tech companies ask about data structures and algorithms in job interviews.
5. Understanding: They help you understand how computers work at a deeper level, making you a better programmer overall.

How to Choose the Right Data Structure or Algorithm

Choosing the right data structure or algorithm depends on your specific problem. Here are some factors to consider:

1. Type of data: Some structures are better for certain types of data (e.g., trees for hierarchical data).
2. Operations needed: Consider what you’ll be doing most often (e.g., inserting, deleting, searching).
3. Time complexity: How fast does the structure or algorithm need to be for your use case?
4. Space complexity: How much memory can you afford to use?
5. Ease of implementation: Sometimes a simpler solution is better, even if it’s slightly less efficient.

Conclusion

Data structures and algorithms are the building blocks of efficient, scalable software. By understanding these concepts, you’ll be better equipped to solve complex problems and write high-quality code. Remember, the best data structure or algorithm depends on your specific needs – there’s no one-size-fits-all solution.

As you continue your programming journey, keep exploring different data structures and algorithms. Practice implementing them, and try to understand their strengths and weaknesses. Over time, you’ll develop an intuition for which tool is right for each job.

Happy coding!